DFA Minimization

First of all, I explain what the finite automata (FA) is. Then I will be defined what is DFA after that I exp how to minimizate DFA.

Finite Automata ( FA )

A finite automaton (FA) is a simple idealized machine used to recognize patterns within input taken from some character set or alphabet. The job of an FA is to accept or reject an input depending on whether the pattern defined by the FA occurs in the input. So we can say Finite Automata(FA) is the simplest machine to recognize patterns.

A Finite Automata consists of the following : Formal specification of machine is : { Q, ∑, q, F, δ }. Q : Finite set of states. ∑ : set of Input Symbols. q : Initial state. F : set of Final States. δ : Transition Function.

We can represent a FA graphically, with nodes for states, and arcs for transitions. We execute our FA on an input sequence as follows:

• Begin in the start state
• If the next input char matches the label on a transition from the current state to a new state, go to that new state
• Continue making transitions on each input
  • If no move is possible, then stop
  • If in accepting state, then accept

Deterministic Finite Automata ( DFA )

Deterministic finite automata - a state machine for which each transition for a state is uniquely determined by it’s input symbol as each state can only have a single move per input symbol. In a DFA, for a particular input character, machine goes to one state only. A transition function is defined on every state for every input symbol. Also in DFA null (or ε) move is not allowed, DFA can not change state without any input character.

Minimization of DFA

DFA minimization stands for converting a given DFA to its equivalent DFA with minimum number of states.

• Draw a table for all pairs of states (Qi, Qj) not necessarily connected directly [All are unmarked initially]
• Consider every state pair (Qi, Qj) in the DFA where Qi ∈ F and Qj ∉ F or vice versa and mark them. [Here F is the set of final states]
• Repeat this step until we cannot mark anymore states − If there is an unmarked pair (Qi, Qj), mark it if the pair {δ (Qi, A), δ (Qi, A)} is marked for some input alphabet.
• Combine all the unmarked pair (Qi, Qj) and make them a single state in the reduced DFA.

Example

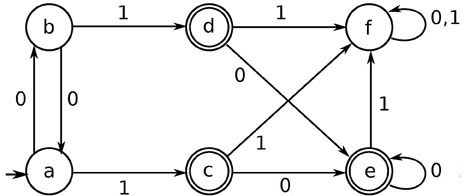
We draw a table for all pair of states.

	a	b	c	d	e	f
a	✓
b		✓
c			✓
d				✓
e					✓
f						✓

We mark the state pairs.

	a	b	c	d	e	f
a
b
c	✓	✓
d	✓	✓
e	✓	✓
f			✓	✓	✓	✓

We will try to mark the state pairs, with green colored check mark, transitively. If we input 1 to state ‘a’ and ‘f’, it will go to state ‘c’ and ‘f’ respectively. (c, f) is already marked, hence we will mark pair (a, f). Now, we input 1 to state ‘b’ and ‘f’; it will go to state ‘d’ and ‘f’ respectively. (d, f) is already marked, hence we will mark pair (b, f).

	a	b	c	d	e	f
a
b
c	✓	✓
d	✓	✓
e	✓	✓
f	✓	✓	✓	✓	✓	✓

After that, we have got state combinations {a, b} {c, d} {c, e} {d, e} that are unmarked. We can recombine {c, d} {c, e} {d, e} into {c, d, e} Hence we got two combined states as − {a, b} and {c, d, e} So the final minimized DFA will contain three states {f}, {a, b} and {c, d, e}

DFA Minimization using Equivalence Theorem

If X and Y are two states in a DFA, we can combine these two states into {X, Y} if they are not distinguishable. Two states are distinguishable, if there is at least one string S, such that one of δ (X, S) and δ (Y, S) is accepting and another is not accepting. Hence, a DFA is minimal if and only if all the states are distinguishable.

• All the states Q are divided in two partitions − final states and non-final states and are denoted by P0. All the states in a partition are 0th equivalent. Take a counter k and initialize it with 0.
• Increment k by 1. For each partition in Pk, divide the states in Pk into two partitions if they are k-distinguishable. Two states within this partition X and Y are k-distinguishable if there is an input S such that δ(X, S) and δ(Y, S) are (k-1)-distinguishable.
• If Pk ≠ Pk-1, repeat previous step, otherwise go to next.
• Combine kth equivalent sets and make them the new states of the reduced DFA.

For the example with step by step

Example

q	δ(q,0)	δ(q,1)
-> a	b	c
b	a	d
* c	e	f
* d	e	f
* e	e	f
f	f	f

Let us apply the above algorithm to the above DFA − P0 = {(c,d,e), (a,b,f)} P1 = {(c,d,e), (a,b),(f)} P2 = {(c,d,e), (a,b),(f)} Hence, P1 = P2. There are three states in the reduced DFA. The reduced DFA is as follows −

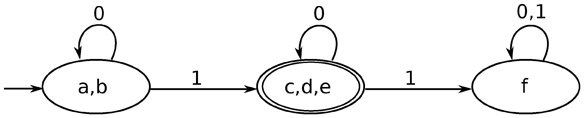
Q	δ(q,0)	δ(q,1)
-> (a,b)	(a,b)	(c,d,e)
* (c,d,e)	(c,d,e)	(f)
f	f	f

Resources

https://www.tutorialspoint.com/automata_theory/dfa_minimization.htm https://www.tutorialspoint.com/automata_theory/deterministic_finite_automaton.htm

Made by Merve TANRIKULU